400-004-0551
- 网站首页
- 解决方案
- 科研实力
-
产品中心
- 量子安全智能办公硬件
- 量子安全高拍仪
- 量子安全笔记本电脑
- 量子安全云智能Pad
- 量子安全云办公一体机
- 量子安全云智能签字笔
- 量子安全手表
- 量子安全智能鼠标
- 量子安全智能工牌
- 量子安全水滴
- 量子安全智能办公软件
- 量子安全办公OA软件
- 量子安全智能印签系统
- 客户&伙伴
- 合作生态
- 视频中心
- 新闻中心
- 关于云玺

news center
新闻中心
发布时间:2023-03-02 11:18:28 信息来源: 阅读次数: 3090 次
导读:
以后如果你看到量子计算机的新闻,千万不要问“计算能力跟我的电脑比起来怎么样”或者“打游戏会卡吗”,人家一听就知道你很外行。如果你问“它针对的是哪个数学问题,把计算量从什么改进到了什么”,人家就知道你是懂行的了。——一般人我不告诉他!
前文参见:
八、量子信息的优势
从以上内容可以看出,量子信息跟经典信息相比有很大的优势。
首先是一个显而易见的优势。前面比喻过:经典比特是“开关”,只有开和关两个状态,而量子比特是“旋钮”,有无穷多个状态。旋钮的信息量显然比开关大得多。
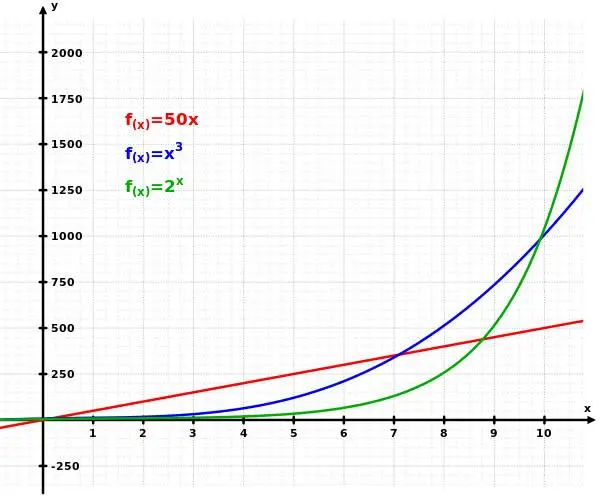
还有一个稍微复杂一点的优势。一个包含n个经典比特的体系,总共有2^n个状态。想知道一个函数在这个n比特体系上的效果,需要对这2^n个状态都计算一遍,总共要2^n次操作。当n很大的时候,2^n是一个巨大的数字。指数增长是一种极快的增长,比n的任何多项式都快。比如说,2^n比n的10000次方增长得还要快。
对n个量子比特的体系,却有一个巧妙的办法。使每个量子比特都处于自己的|+> =(|0> + |1>)/√2态,那么整个体系的状态就是|++…+> = (|00…0>+ |00…1> + … + |11…1>) /2^(n/2)。(根据定义就可以知道,这是个直积态,不是纠缠态,虽然它确实是一个叠加态。纠缠态和叠加态是两个概念。)仔细看看你会发现,0和1的所有长度为n的组合都出现在其中,总共有2^n项,刚好对应n个经典比特的2^n个状态。对这个叠加态做一次操作,得到的就是所有2^n个结果的叠加态。量子比特的一次操作,就达到了经典比特2n次操作的效果!
但在欢呼之前,我们需要认清,这个巨大的优势并不容易利用。因为所有2n个结果是叠加在一起的,读取出来需要做测量,而一做测量就只剩下一个结果,其余的结果都被破坏了。所以我们只能把这个优势称为潜在的巨大优势,真要利用它,需要非常巧妙的算法。
这样的算法只对少数的问题能够设计出来,后面会举一些例子,如“因数分解”。有些科普文章把量子计算机描写成无所不能,快成神了,这是重大的误解。量子计算机的强大,是与问题相关的,只针对特定的问题。
九、量子信息的应用
前面说过,量子信息的研究内容包括量子通信和量子计算。从这两个名字我们立刻就可以发现,量子信息还没有进入生活,因为大家都还在用经典的电脑和手机呢。具体地说,量子通信已经有了一些实际应用,量子卫星就是做相关实验的。而量子计算的发展程度要低得多,还处于演示阶段,尚未造出有实用价值的量子计算机。
量子信息究竟能用来干什么呢?下面我们来介绍量子信息的四项应用。在量子计算方面,有量子因数分解(破解最常用的密码体系)和量子搜索(用途最广泛的量子算法)。在量子通信方面,有量子隐形传态(“传送术”,最富有科幻色彩的应用)和量子密码术。在所有这些应用中,量子密码术是目前唯一接近实用的,但这一个就非常重要,足以表现量子信息的价值了。
十、量子因数分解和密码破解
所谓因数分解,就是把一个合数分解成质因数的乘积,例如21 = 3 × 7。因数分解是数学中的经典难题。
你也许会问,这有什么难的?你当然不管三七二十一就能分解21,但请试试看分解2^67 - 1 =147,573,952,589,676,412,927。这是个18位数。1644年(明朝灭亡的那一年),法国数学家梅森(Marin Mersenne)提出它是一个质数。在那之后的很长时间里,人们都这么认为。直到1903年(清朝都快亡了),人们才发现它是一个合数,等于193,707,721 ×761,838,257,287。耗了一个朝代!
让我们想想,如何分解一个数字N。最容易想到的算法,是从2开始往上,一个一个地试验能否整除N,一直到N的平方根为止。如果N用二进制表示是个n位数,即N约等于2n,那么尝试的次数大致就是2n/2。这是指数增长的计算量,前面说过,指数增长是一个灾难。
在计算机科学中,把计算量指数增长的问题称为“不可计算的”,把计算量多项式增长的问题称为“可计算的”。不可计算的意思并不是计算机不能算,而是计算量增长得太快,很容易就达到“把全世界的计算机集中起来算几十亿年都无法得出结果”的程度。
当然,计算量是跟算法有关的,你可以寻找效率更高的算法,也应该这么做。对于因数分解,“从2开始一个一个试”并不是最聪明的算法。在经典计算机的框架中,目前最好的算法叫做“数域筛”,计算量有所减少,但仍然是指数增长。
“艾数学”同学,你想问数域筛的计算量具体是多少?一般人我不告诉他,答案是exp[O(n^(1/3) log^(2/3)n)](在数学中,大写字母O后面跟一个式子,表示结果跟这个式子具有同样的数量级)。
这样的计算量是什么概念?如果计算机一秒做1012次运算,那么分解一个300位的数字需要15万年,分解一个5000位的数字需要……50亿年!地球的年龄也不过是46亿年而已!
由此可以看出因数分解的一个特点:它的逆操作,即算出两个质数的乘积,是非常容易的;而它本身,却是非常困难的。这种“易守难攻”的特性,使它在密码学中得到了重要的应用。
密码学的基本框架,我们会在后面介绍量子密码术时阐述。在这里,我们只需要指出一点:因数分解的困难性,是现在世界上最常用的密码系统“RSA”的基础。RSA这个名字,是三位发明者李维斯特(Ron Rivest)、萨莫尔(Adi Shamir)和阿德曼(Leonard Adleman)的首字母缩写。

RSA是一种“公开密钥密码体系”,它的密钥(即加密时用到的参数)是对全世界所有人公开的。为什么敢公开?因为这个密钥是一个很大的合数,解密需要把它分解成两个质数,而发布者有信心别人在正常的时间内解不开。
但是RSA有两大隐患。第一点,我们只是知道目前公开的最好的算法是数域筛,但不知道是否有更好的算法。更令人寝食不安的是,某些国家、某些组织也许已经掌握解密的算法了,只是没有告诉你!
第二点,上面说的算法都是在经典计算机上运行的,“最快的算法都无法破解RSA”指的是经典计算机。对于量子计算机,我们却已经知道了它可以破解RSA。
如前所述,量子计算相对于经典计算有潜在的巨大优势,只是实现这种优势需要聪明的算法设计,只有对少数问题能够设计出这样的算法。而因数分解,就是这样的问题之一。1994年,肖尔(Peter Shor)发明了一种量子算法,把因数分解的计算量减少到了多项式级别,也就是从不可计算变成了可计算。
艾数学同学,你又在举手了?嗯,肖尔算法的计算量是O(n^2 logn loglogn),一般人我不告诉他。
这又是个什么概念呢?同样还是分解300位和5000位的数字,量子算法会把所需时间从15万年减到不足1秒钟,从50亿年减到2分钟!对RSA密码系统来说,这不是“隐”患,而是“明”患!
看起来,全世界的密码人员都应该陷入恐慌了。但事实上还没有,人们仍然在用着RSA。为什么呢?因数分解的量子算法只是理论,真要实现它还是非常困难的,造出有实用价值的量子计算机还需要很多努力。
第一次真正用量子算法分解质因数是在2007年实现的,把15分解成3 × 5。有两个研究组同时做出了这个实验,一个是中国科学技术大学的潘建伟和陆朝阳等人,一个是澳大利亚布里斯班大学的A. G. White和B. P. Lanyon等人。此后各国科学家不断努力,把这个领域推向前进。目前在实验上分解的最大的数是291,311 = 523 × 557,是由中国科学技术大学的杜江峰和彭新华等人在2017年实现的。
什么,你前边跟我说量子算法随随便便就能分解几千位的数字,结果实际上最大只能分解一个六位数?你是在耍我吗?
这位同学,请你先把手里的刀放下……同学们,一定要分清潜力和现状。火车刚出现的时候,跑得没有马车快,还经常出故障。但是任何有洞察力的人都能看出,火车代表着未来,因为它能够达到的上限远远超过马车。RSA现在当然还可以用,但达摩克利斯之剑已经悬挂起来了,任何有责任心的密码人员都会时刻关心量子计算的进展。
还有一点值得注意的是,造出专门处理某些任务的“专用”的量子计算机比造出“通用”的量子计算机要容易得多。专用的东西比通用的容易造,这是一个普遍规律。在可编程的电子计算机出现之前300多年,冈特(Edmund Gunter, 1581-1626)和奥特雷德(William Oughtred, 1574-1660)就造出了计算尺。
谷歌宣布计划在2017年造出超越传统计算机的量子计算机,很可能指的就是这种专用计算机。斯诺登从美国出逃后,披露了美国国家安全局有一个绝密的项目“穿透硬目标”(Penetrating Hard Targets),计划建造一台专用于破解密码的量子计算机。据传该局已经存放了大量外国政府的密电,一旦项目成功立刻对它们动手。这足以让其他国家不寒而栗了!
同样的道理,2017年5月,中国科学技术大学潘建伟和陆朝阳等人宣布造出世界上第一台超越早期电子计算机的光量子计算机,也是特别针对一个问题的,这个问题叫做“玻色子取样”。对它的量子算法,也是把指数增长的计算量缩减到了多项式增长的计算量。成果就是,这台量子计算机算起玻色子取样来,比第一台电子管计算机ENIAC和第一台晶体管TRADIC快了10到100倍。
顺便提一下,有些人迷惑光量子计算机跟量子计算机是什么关系,甚至还有人说光量子计算机不是量子计算机。实际上,量子计算机总需要用某种物理体系来实现,好比电子计算机可以用电子管实现,也可以用晶体管实现,甚至可以像《三体》中设想的那样用几千万人来实现(秦始皇:有人叫我?)。光量子计算机就是用光子作为量子比特的量子计算机。除了光子之外,量子计算机常用的物理体系还包括光学共振腔、离子阱、核磁共振等等。没关系,你不需要现在就看懂这些物理学术语……


以后如果你看到量子计算机的新闻,千万不要问“计算能力跟我的电脑比起来怎么样”或者“打游戏会卡吗”,人家一听就知道你很外行。如果你问“它针对的是哪个数学问题,把计算量从什么改进到了什么”,人家就知道你是懂行的了。——一般人我不告诉他!
(未完待续)
背景简介:本文作者为袁岚峰,中国科学技术大学化学博士,中国科学技术大学合肥微尺度物质科学国家实验室副研究员,科技与战略风云学会会长。